Sfida problema: i ponti di RE 10

Durante il lavoro sui pari e dispari (vedi qui e qui) continuava a ronzarmi in testa l'idea di affrontare la topologia. In un primo momento continuavo ad accantonare questo pensiero perché mi sembrava una mezza pazzia proporre l'argomento, vista la difficoltà. Poi mi sono detta "ok proviamoci, male non farà!". Sono andata a rivedere il materiale fornitomi dalla mia cara amica  Cristina Sperlari durante uno dei nostri corsi di aggiornamento e ho preparato il lavoro. Così una mattina è arrivata posta: una nuova richiesta di aiuto da RE 10! 

Cari bambini devo di nuovo chiedere il vostro aiuto. I contadini Bepi e Toni devono vendere al mercato i loro ortaggi. Il mercato è lontanissimo dalla reggia e per raggiungerlo devono attraversare la città. La città è divisa in due dal grande fiume Numerino che nel centro forma anche due isolette. Per collegare le due isole tra loro e con la terra ferma sono stati costruiti 7 ponti. Ho bisogno di aiuto perché Bepi e Toni stanno litigando furiosamente: Bepi sostiene che è possibile attraversare ogni ponte 1 sola volta in modo da ritornare al punto di partenza.  Toni dice che non è così. Chi ha ragione? Finché non troviamo una soluzione nessuno dei due tornerà a coltivare le verdure dell’orto!!! La loro amicizia è in pericolo! Vi mando la mappa della città per aiutarvi a trovare la soluzione.       RE 10

Ho consegnato subito ai vari gruppi il messaggio del RE e ascoltato i loro commenti (come al solito molto divertenti!):

"che strano: una richiesta facilissima!"

"maestra vedrai che li aiutiamo in un attimo"

"sì così dopo possiamo fare il lavoro che ci hai preparato per oggi"

"non è possibile che Bepi e Toni non ci siano riusciti"

"ok ci tocca aiutare RE 10 ancora una volta!"

😂😂😂

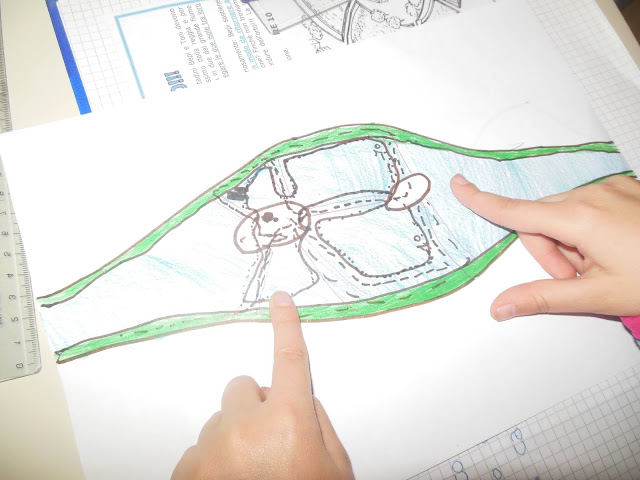
Abbiamo letto insieme la lettera e cercato di capire bene qual era la richiesta aiutandoci con il disegno allegato:

Analizzando il messaggio abbiamo concluso che il nostro compito doveva consistere nel verificare:

📌 se esiste un modo per fare il giro dei 7 ponti senza ripassare MAI per la stessa strada;

📌 se è possibile che arrivo e partenza coincidano.

I bambini hanno subito provato a disegnare percorsi con la matita direttamente sulla scheda consegnata, ma si sono persi immediatamente. Allora ho proposto di rifare alla lavagna il disegno in modo un po' più schematico per visualizzare meglio e subito solo gli elementi importanti:

Dopodiché ogni gruppo ha provato su un foglio a rifare il disegno (più o meno schematico) e a disegnare le stradine con colori diversi:

Hanno disegnato e provato percorsi per circa mezzora, chiedendo anche più fogli di malacopia. Ogni tanto si levava un grido: 
📌 "abbiamo trovato la soluzione!" 
📌 "si può" 
📌 "ce l'abbiamo fatta" 
e ogni volta immancabilmente, quando mi avvicinavo per controllare, scoprivamo che non era così😂! Dopo un po' hanno iniziato a chiedermi: 
📌 "maestra ma c'è la soluzione?" 
📌 "certo!" 
📌 "tu l'hai trovata?" 
📌 "si, l'ho trovata dando solo uno sguardo!" 😈😈😈 
📌 "ecco, sei un genio!" 
📌 "come al solito tu sai fare tutto" 
📌 "sei veramente speciale: per te non c'è nulla di difficile" 😂 

Ad un certo punto tutta la classe ha protestato affermando che non trovavano la soluzione e quindi forse non c'era perché - come disse Viola - "c'è sempre un ponte che dà fastidio!"💪💪💪Era arrivato il momento di intervenire e rassicurarli: la soluzione è che non c'è soluzione! Questo concetto è molto spiazzante per i bambini abituati a risolvere calcoli e utilizzare algoritmi ed è di difficile comprensione:  

📌 "allora RE 10 ci ha imbrogliato!" 
📌 "era un trabocchetto!" 
📌 "ma siamo sicuri che è proprio così?" 
📌 "come si fa a dimostrare che non c'è soluzione?" 
Questa domanda mi ha riempito di gioia visto che da inizio prima cerco di far  capire ai bambini non solo "come si fa" ma anche "perché si fa"!
A questo punto ho confessato: 
"cari bambini, secondo me RE 10 vi ha fatto un bello scherzo: il problema dei ponti è un famosissimo problema studiato dal grande matematico Eulero nel 1700 (circa 300 anni fa)!" 
E' stata una bella occasione anche per parlare un po' di storia della matematica e di uno dei matematici famosi del passato, così ho raccontato alla classe per sommi capi chi era Eulero e perché è famoso: 

Relativamente al problema presentatoci da RE 10, ho chiarito che è ispirato ad una situazione reale: la città di Konigsberg è percorsa dal fiume Pregel e presenta due grandi isole che sono collegate tra di loro e con le terra ferma da 7 ponti. Nel corso dei secoli è stata più volte posta la questione se fosse possibile con una passeggiata seguire un percorso che attraversi ogni ponte una volta soltanto. Nel 1736 Eulero affrontò questo problema dimostrando che la passeggiata non era possibile. Eulero non si limitò a dire che non era possibile, ma trovò una dimostrazione cioè una regola matematica per spiegarlo ( ... e qui entrano in ballo i pari e dispari!!!). Per prima cosa riprodusse la mappa della città in modo più semplice e schematico, poi semplificò ulteriormente lo schema con punti (vertici o nodi) e linee (spigoli):

Ecco la nostra rappresentazione nel quaderno:

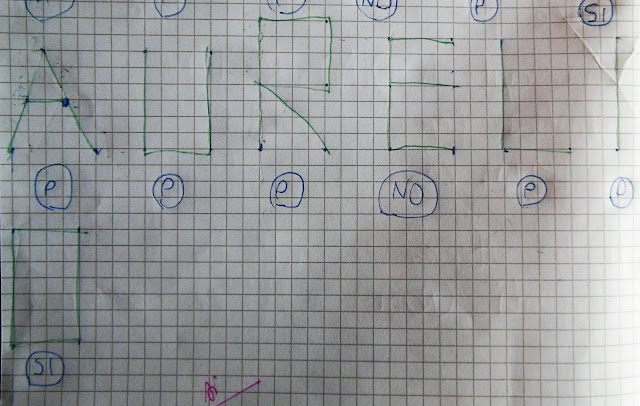
Abbiamo verificato sul disegno quanti spigoli partano/arrivino ad ogni nodo e se il numero è pari o dispari. Vista la difficoltà di comprensione dell'argomento ho proposto di disegnare altri grafi molto semplici alla lavagna e di analizzarli per scoprirne la percorribilità: è possibile percorrerlo passando per i nodi una sola volta? partenza e arrivo coincidono? Dopo molti esempi alla lavagna abbiamo provato nel quaderno con le lettere dell'alfabeto stilizzate, con i nomi di Eulero, dei maestri e di tutti i bambini (si possono usare anche i numeri):

Il lavoro sui nomi è stato significativo e ha permesso a quasi tutti di capire bene i concetti e imparare anche il linguaggio specifico:

📌 "maestra hai ragione: basta uno sguardo per capire ora che sappiamo il trucco!"😂

📌 "mi è piaciuto questo lavoro"

📌 "abbiamo scoperto un sacco di cose nuove"

📌 "adesso a casa sfido il papà: sicuramente non lo sa fare e lo stupirò"

Un grazie anche ai genitori geometri e ingegneri della classe che queste cose le masticano ... ma sono stati al gioco 😎!!!

Nei giorni successivi ho anche fornito ai bambini la scheda della prossima foto (fornitami sempre da Cristina durante l'aggiornamento) e ho chiesto ai bimbi  - divisi in gruppi - di verificare la percorribilità dei vari percorsi cittadini (REALI): sono stati bravissimi💪 ... molto più di me che quando ho affrontato da corsista lo stesso lavoro inizialmente non capivo niente 😥!!! ... ma questo resterà un segreto tra me, voi e Cristina!!!

E poi per concludere ecco come hanno passato le merende nei  giorni successivi💪: giocando a inventare grafi e sfidandosi a capirne la percorribilità!

A conclusione ho proposto la seguente scheda (usata poi anche come verifica):

😎 Che dire ancora? Super soddisfatta di averci provato e del percorso fatto dai bimbi! Non credevo possibile proporre in modo significativo questo lavoro, ma con l'aiuto di Cristina ci sono riuscita (grazie in eterno cara 😘) e i risultati sono stati veramente eccellenti. Ho una mezza idea di riprendere l'argomento il prossimo anno aggiungendo alla storia due personaggi: il Principe Rosso e il Principe Blu ... vedremo😉!
Stay tuned ...