Pi Greco Day in classe terza ... al tempo del Coronavirus! (2° parte)

Nel post precedente (qui) avevo pubblicato la sfida problema per festeggiare da casa il Pi Greco Day! Con enorme mia soddisfazione ben 18 piccoli alunni - con la collaborazione dei loro meravigliosi genitori - mi hanno inviato le foto del lavoro eseguito: un ottimo lavoro 💪💪💪 !!! 

Riporto il testo della prova per chi lo avesse perso:

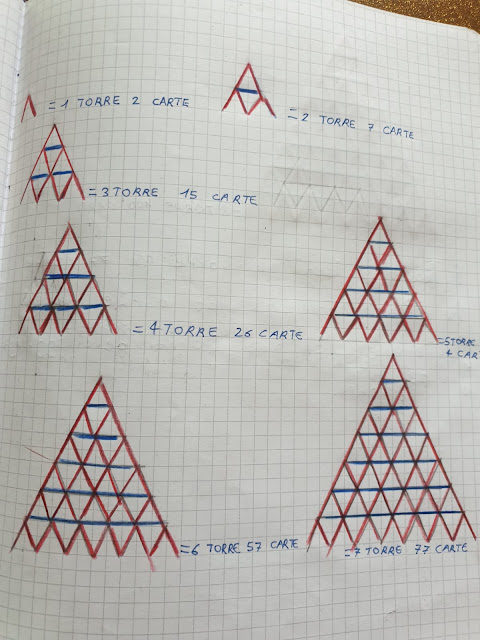
LE TORRI Giorgio costruisce torri con le carte, seguendo lo schema della figura. La prima torre è stata realizzata con 2 carte, la seconda con 7, la terza con 15 e così via. Quante carte dovrebbe aggiungere alla decima torre per ottenere l'undicesima?

📌 LA STRADA PIÙ SEMPLICE

La maggioranza dei bambini (8) ha disegnato tutte le torri e contato quante carte sono servite per costruire ogni torre, arrivando in modo particolare alla settima e all'ottava:

·         7° torre → 77 carte

·         8° torre → 100 carte

quindi 100 – 77 = 23

La conclusione trovata è che per costruire l’ottava torre basta aggiungere 23 carte alla settima. Riporto qui l'esempio più chiaro tra gli otto che mi sono arrivati:

📌 UNA STRADA UN PO’ PIÙ IMPEGNATIVA 

Tre bambini invece di costruire tutte le torri, ne hanno costruita una sola aggiungendo via via le carte necessarie per ingrandirla e passare alla successiva. “Cambiando” torre hanno contato le carte giungendo comunque alla soluzione corretta! Veramente bravi 💪💪💪! Ecco due esempi:

★ bambino 1:

★ bambino 2:

📌 UNA STRADA MOLTO IMPEGNATIVA

Disegnando le torri 3 bambini si sono accorti che la base della torre è fatta da un modulo di 2 carte che si ripete:

In questo modo hanno analizzato le basi scoprendo che:

·         1° torre → 1 modulo di 2 carte → 2 carte totali

·         2° torre → 2 moduli di 2 carte → 2 x 2 = 4 carte totali

·         3° torre → 3 moduli di 2 carte→ 3 x 2 = 6 carte totali

·         4° torre → 4 moduli di 2 carte→ 4 x 2 = 8 carte totali

·         5° torre → 5 moduli di 2 carte→ 5 x 2 = 10 carte totali

·         6° torre → 6 moduli di 2 carte→ 6 x 2 = 12 carte totali

·         7° torre → 7 moduli di 2 carte→ 7 x 2 = 14 carte totali

·         8° torre → 8 moduli di 2 carte→ 8 x 2 = 16 carte totali

Il ragionamento si è quindi focalizzato sulla riga di moduli che formano la base del castello perché le righe superiori mantengono lo stesso numero di carte. In questo modo basta variare e poi contare il modulo della base a cui si aggiungono le carte del tetto:

·         1° torre → 2 carte della base

·         2° torre → 2 moduli di 2 carte → (2 x 2) + 1 tetto = 4 + 1 = 5 carte

·         3° torre → 3 moduli di 2 carte→ (3 x 2) + 2 carte tetto = 6 + 2 = 8 carte

·        4° torre → 4 moduli di 2 carte→ (4 x 2) + 3 carte tetto = 8 + 3 = 11 carte

·    5° torre → 5 moduli di 2 carte→ (5 x 2) + 4 carte tetto = 10 + 4 = 14 carte

·    6° torre → 6 moduli di 2 carte→ (6 x 2) + 5 carte tetto = 12 + 5 = 17 carte

·    7° torre → 7 moduli di 2 carte→ (7 x 2) + 6 carte tetto = 14 + 6 = 20 carte

·     8° torre → 8 moduli di 2 carte→ (8 x 2) + 7 carte tetto = 16 + 7 =23 carte

Vediamo degli esempi:
★ bambino 1:

★ bambino 2:

★ bambino 3:

📌 UNA REGOLARITÀ INTERESSANTE (3 bambini)

Tre bambini hanno fatto una scoperta: la differenza tra la somma di carte tra una torre e l’altra è sempre di + 3:

★ bambino 1:

★ bambino 2:

★ bambino 3:

📌 RAGIONAMENTO PER “MODULI LATERALI" 

Due bambini hanno individuato un altro modulo: hanno contato i triangoli laterali che formano ogni torre togliendo 1 pavimento! Riporto in foto il lavoro di un alunno la cui argomentazione è assolutamente corretta ma non molto chiara. Per aiutare tutti nella comprensione riporto anche la mia successiva spiegazione:

Considerazioni finali:

🏆 18 alunni su 22 hanno inviato il lavoro: grande soddisfazione personale in questo momento di didattica a distanza dove lavorare è diventato faticoso e "pesante". Un enorme grazie ai genitori che hanno collaborato, quanto meno per l'invio del materiale!

🏆 Su 18 bambini, 9 hanno lavorato completamente da soli, gli altri con la mediazione dell'adulto.

🏆 Su 18 solo un lavoro evidenzia un ragionamento scorretto e due invece un ragionamento adeguato ma con errori di calcolo.

🏆 Le soluzioni proposte evidenziano il PROCESSO più che la soluzione numerica, con lodevoli tentativi di trovare una regola certa, chiara ed economica. Era proprio quello che speravo! Soddisfazioni enormi perché dopo due anni di lavoro specifico sull'argomentazione e sulla ricerca dei "perché?" invece del "quanto fa?" mi sembra che i bambini abbiano sviluppato una buonissima consapevolezza rispetto al compito, alla consegna nonché all'importanza di cercare soluzioni.

Insomma ... anche sta volta obiettivo raggiunto 💪💪💪 !!!