Siamo a gennaio e non abbiamo ancora ripassato le frazioni ne introdotto i numeri decimali. Il problema, tratto sempre dal papiro di Rhind, è in realtà molto semplice ma con queste premesse credevo avrebbero faticato. Invece sono stati bravi e hanno capito subito che era necessario lavorare graficamente utilizzando le frazioni. Vediamo cosa hanno prodotto in gruppo.
🚩 5 gruppi hanno lavorato nello stesso identico modo, con rappresentazioni grafiche molto simili:
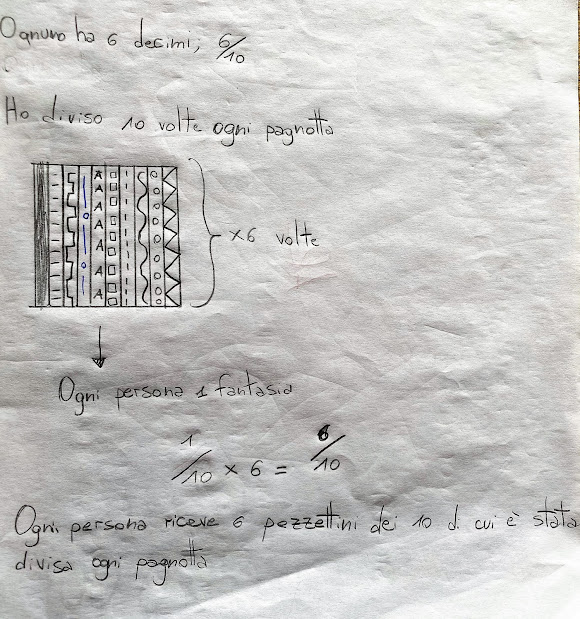
🚩 questa bambina (eseguito completamente da sola perché a casa) ha frazionato solo un panino in 10 parti, stabilendo che ad ogni persona spetta 1/10; successivamente ha moltiplicato 1/10 per 6, dato che i panini sono 6 😍😎💪 :
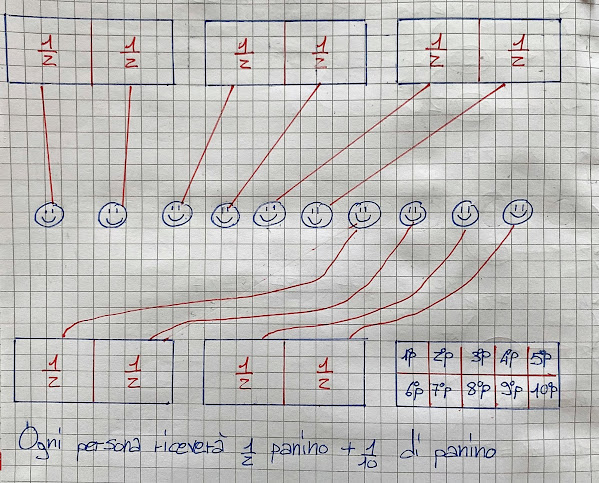
🚩 questo gruppo ha operato in modo ancora diverso: ha deciso di frazionare l'intero (in questo caso composto da 5 panini e non da 6!!!) per trovare le parti equivalenti da distribuire alle 10 persone. Solo allora ha diviso il panino restante in 10 decimi in modo da avere una parte per ogni personaggio.
Ho fatto notare ai bambini che secondo me la rappresentazione grafica non era chiarissima perché:
❌ innanzitutto troppi simboli difficili da gestire e il foglio "troppo pieno" non aiutava la comprensione a colpo d'occhio del loro operato. Mi hanno risposto che probabilmente avevo ragione e che in un paio di occasioni si erano confusi e avevano dovuto contare di nuovo dall'inizio. Dopo aver riflettuto hanno dichiarato che effettivamente sarebbe bastato colorare in modo diverso invece di scrivere un sacco di lettere.
❌ in secondo luogo ho loro indicato che avevano disegnato il 6° panino più grande rispetto agli altri e ho chiesto se erano sicuri di aver diviso equamente per non fare torto a nessuno. Mi hanno risposto che i primi 5 panini erano equivalenti e quindi erano sicuri di aver distribuito correttamente ma che l'ultimo panino poteva essere sia più grande che più piccolo, tanto andava frazionato da solo (è un'unità a se stante secondo loro 😂😂😂) purché le parti tagliate siano tra loro equivalenti e non in relazione altri altri pani. Alla fine hanno anche aggiunto che il testo del problema non era chiaro 😆 perché non indicava affatto che i panini erano uguali!!!
❌ per concludere ho fatto notare che non capivo affatto la scrittura finale che avevano riportato di sette dodicesimi e si sono accorti che effettivamente i conti non tornavano!!! (Ci torneremo tra pochi giorni quando affronteremo un nuovo viaggio nel fantastico mondo delle frazioni ...).
Nonostante alcune incertezze comunque anche questo gruppo ha dimostrato di aver compreso la richiesta e di saper elaborare una strategia risolutiva originale.
Anche sta volta molto soddisfatta 💪💪💪 !








Commenti
Posta un commento